|
|
| This classifier is designed by Mohamed Rafik Bouguélia during his thesis from September 2011 and August 2014. It is an on line learning method based on the "growing neural gas" algorithm (GNG). At each time, only one data is read from a continuous data stream. This data is used to incrementally update the model. The method maintains a model as a dynamically evolving graph topology of data-representatives called neurons. It also performs a merging process which uses a distance-based probabilistic criterion to eventually merge neurons. In the following, we present the different evolutions of this approach. |
|
|
The main point of GNG is its use of a period for the creation of a new node. Different variants of GNG have been proposed to relax this
this periodical evolution.These variants are: IGNG, I2GNG and SOINN. The figure below illustrates the functioning of
each one of them.
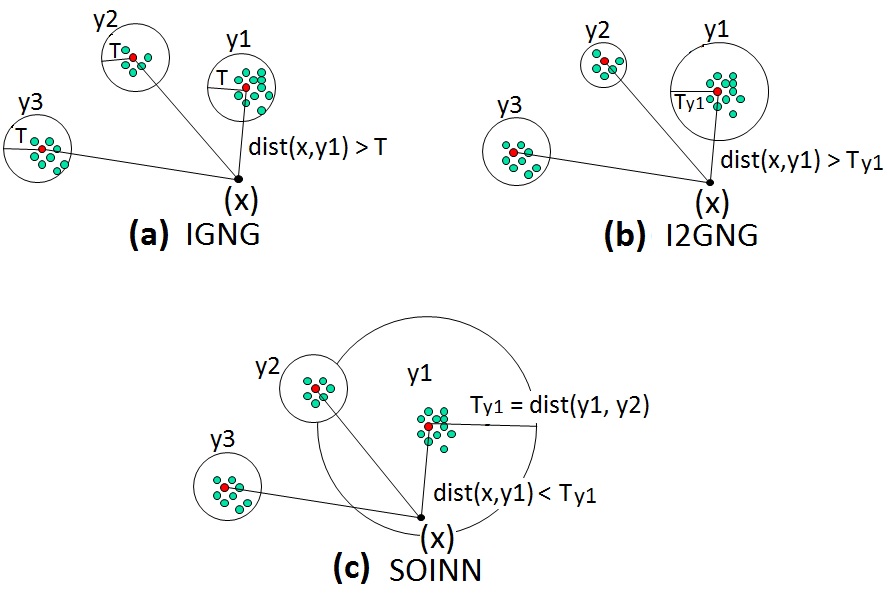 |
|
|
The algorithm
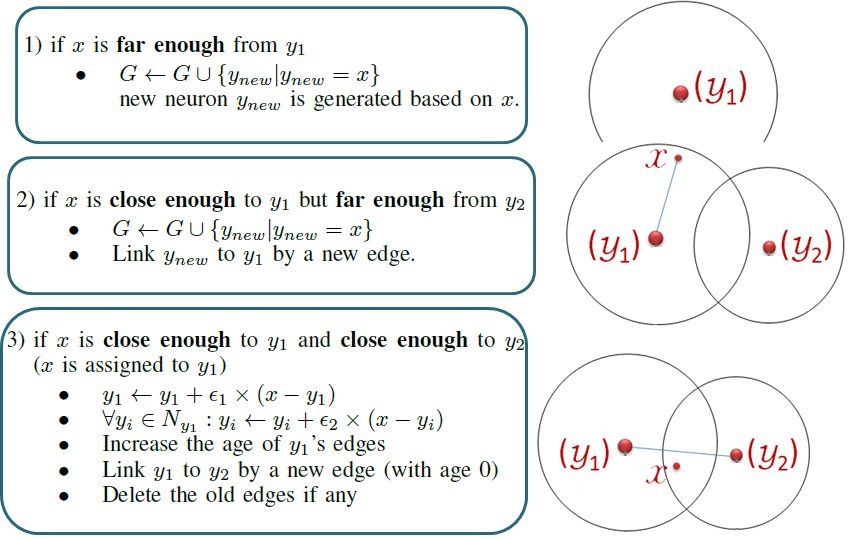
|
The merging process
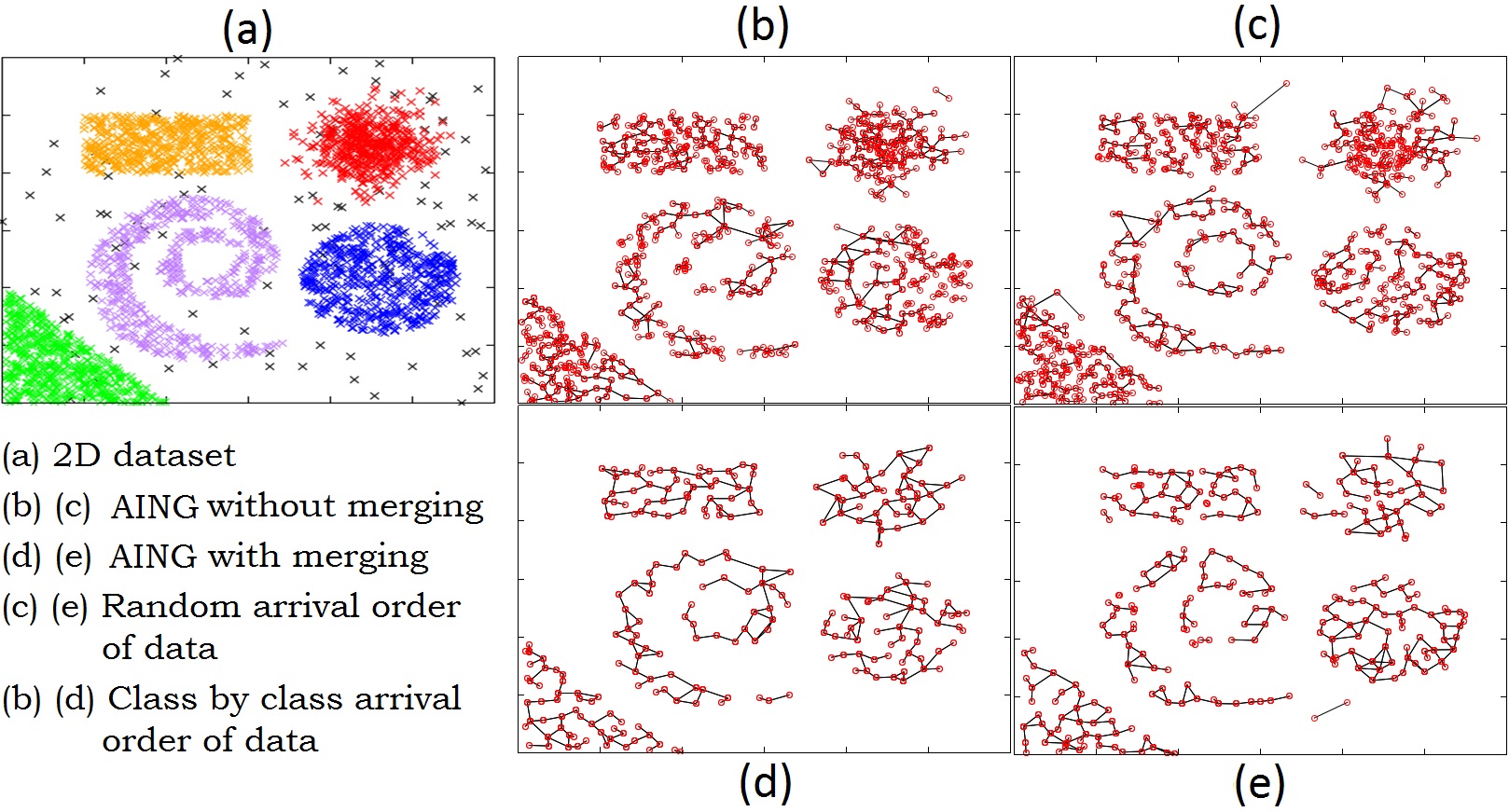 Results 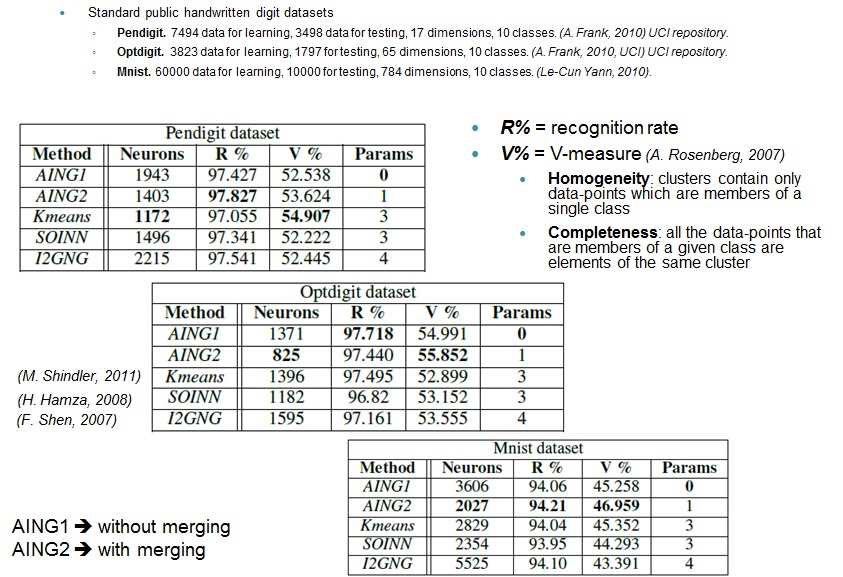 |
|
|
|
The principle
In usual supervised learning methods, data labelling is operated beforehand over a static dataset. This is not possible in the case of data streams where data is continuously arriving. Furthermore, manual labelling is costly and time consuming. Active learning has as objective to adapt the labelling to the contious data stream each time is necessary by querying from a human labeller only the class labels of data which are informative. |
The main actions
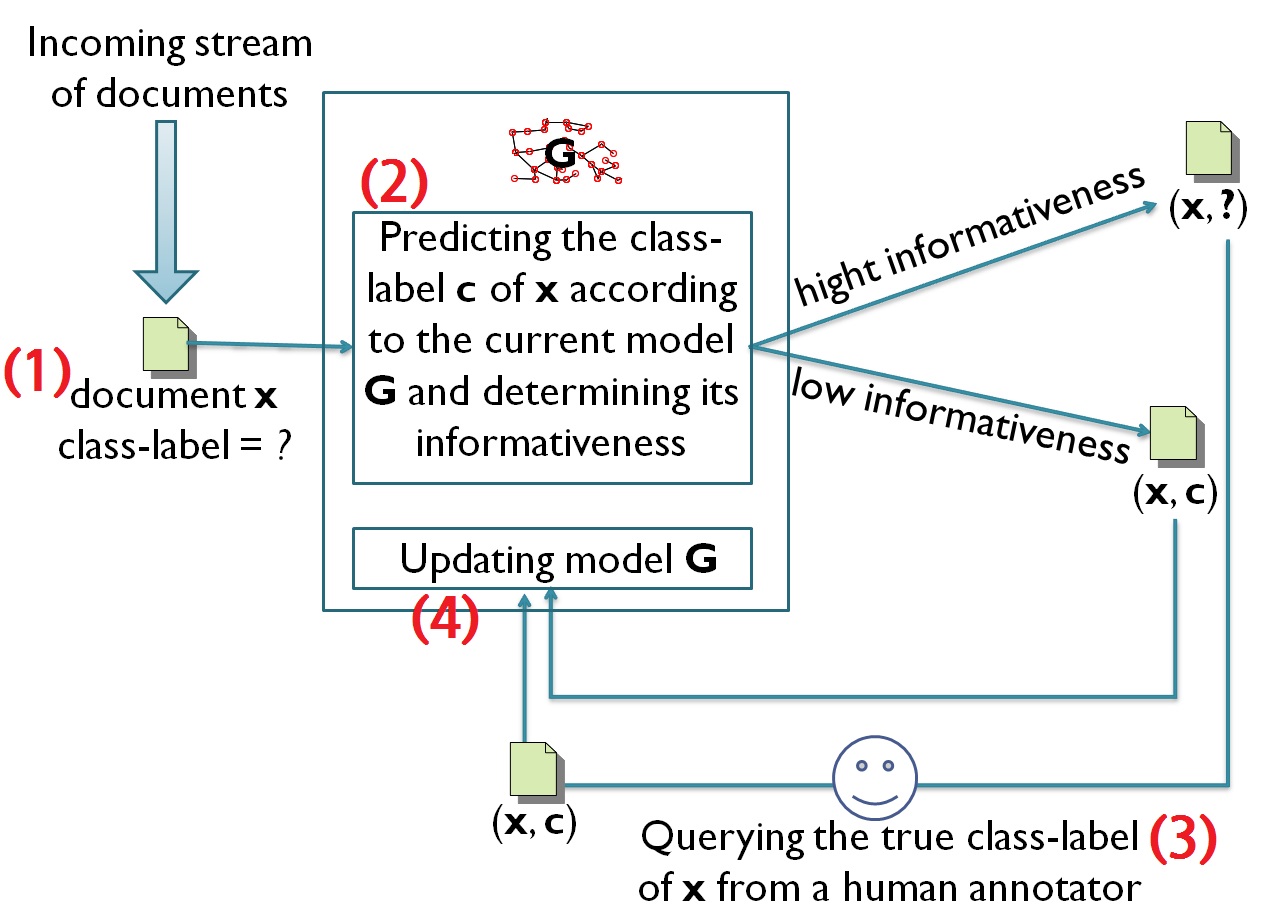 How to label a new class? For each new pattern x, we use K-NN and we derive a probability of belonging to its two most probable classes. Let KNN(x) = {(y1; cy1 )... (yK; cyK)} be the K nearest neurons selected from G. Let P(cjx) be the probability that the pattern x belongs to the class c.  If for a pattern x, Δ(c1;c2|x) is close to 0, this means that the probability of x to belong to both classes are similar and x is informative, because knowing the label of x can help to descriminate from the two classes. Datasets
Experiments 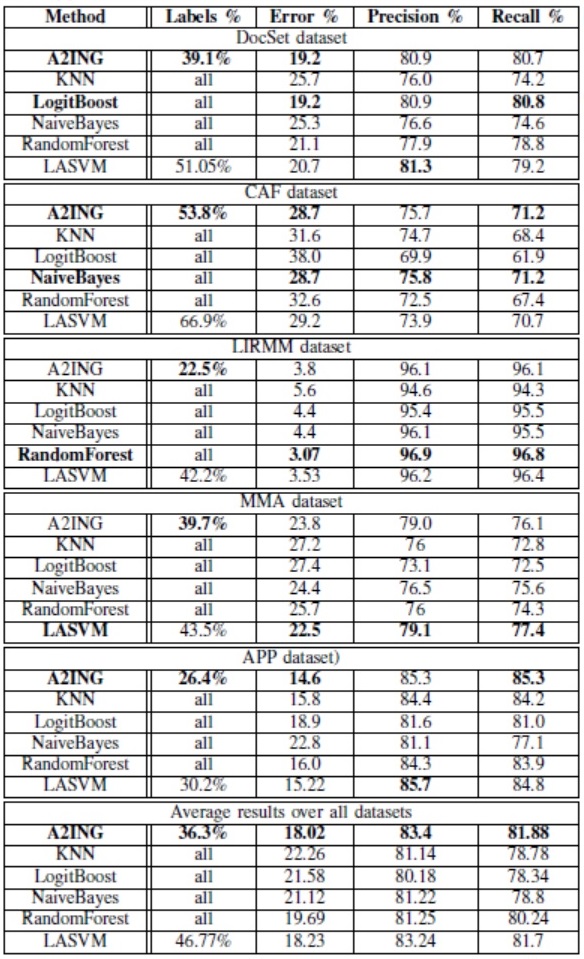 |
|
|
|
Mislabelling is a big issue in active learning methods because it impacts the classification accuracy. M. Rafik Bouguelia proposes a mislabelling likelihood measure to characterize the potentially mislabelled instances. Then, he derives a measure of informativeness that expresses how much the label of an instance needs to be corrected by an expert labeller. Incertainty measure The instances that are selected for manual labelling are typically those for which the model h is uncertain about their class. Given a sample x, the true class label of x would improve h and reduce its overall uncertainty (x is said to be informative) An uncertainty measure that selects instances with a low prediction probability can be defined as:  Impact of label noise M. R. Bouguelia measures below the different impacts of δ over accuracy (A), number of labelled instances (B) and (C) 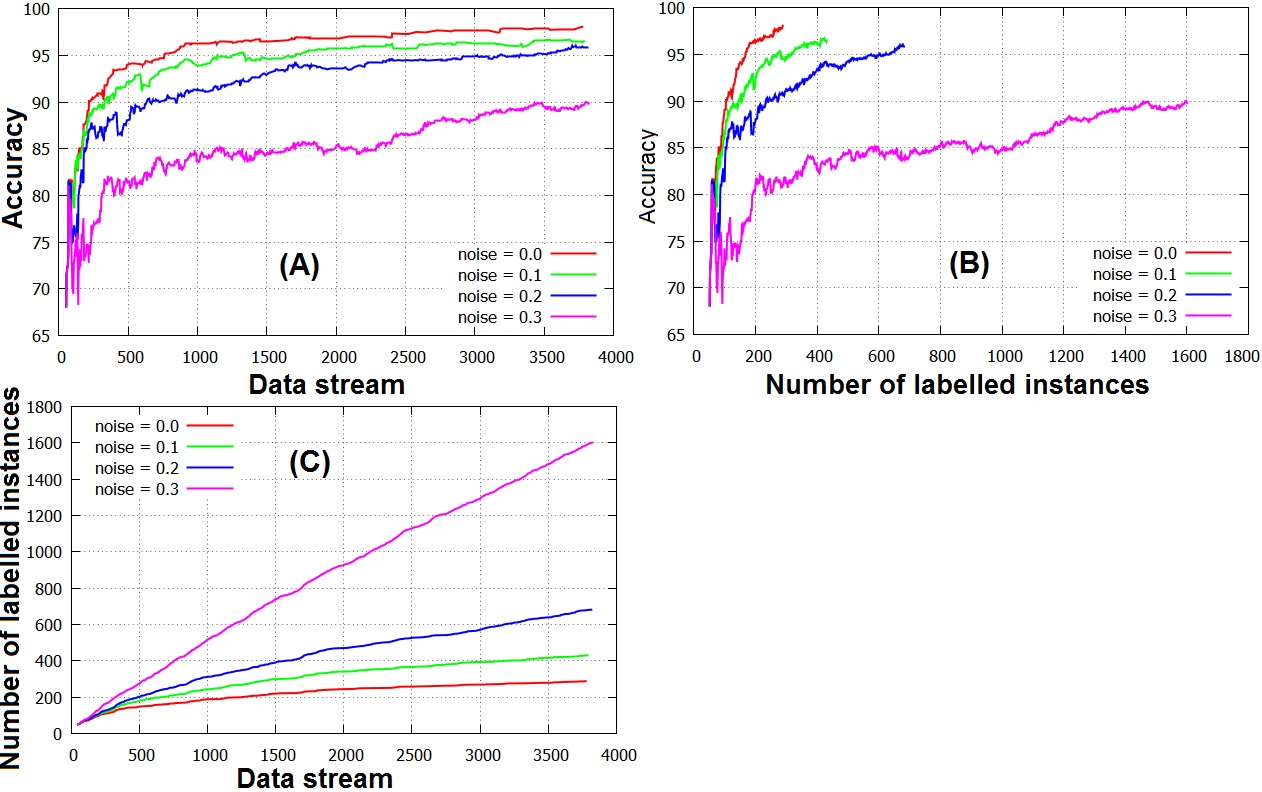 Characterizing mislabelled of instances We define a disagreement coefficient that reflects the mislabelling likelihood of instances. Let x be a data point whose label is queried. The class label given by the labeller is noted yg. Let yp = argmaxy∈Y Ph(y|x) be the class label of x which is predicted by the classifier First measure of disagreement: likelihood disagreement If yg≠yp a mislabelling error have been occurred. Let pp = P(yp|x) and pg = P(yg|x).We estimate a degree of disagreement D1(x) = 1- P(yg|x)⁄P(yp|x) The higher the value of D1, the more likely that x has been incorrectly labelled with yg, because the probability that x belongs to yg would be small relatively to yp. Second measure of disagreement: multiview disagreement Many problems in machine learning require datasets for multiple views, e.g, an object can be categorized from either its color or shape. When the sample in each view doesn't lead to the same class, due to data corruption or noise, this causes a view disagreement. If we consider the features taken by the object in each view, suppose f1 for the first view and f2 in the second view. If we also consider qygfi resp. qypfi the rate that shows how much the feature fi is likely to contribute at classifying x into yp and yg respectively. Let Fp be the set of features that contributes at classifying x in the predicted class yp more than the given class, and inversely for Fg: The quantity information measuring the membership of x to yp (resp. yg) is measured by a second degree of disagreement: 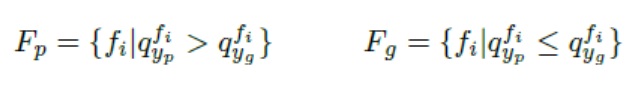 |